Rubyで最短経路を探索しよう！

次に同じ質問がきたときに、

「1時間いらないっしょ、こんなの」

と是非ともほざくために、今から勉強します。

ダイクストラ法による最短経路探索

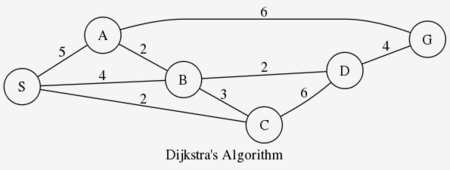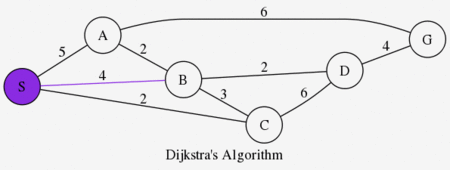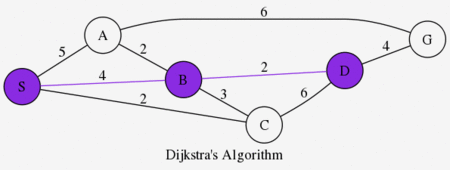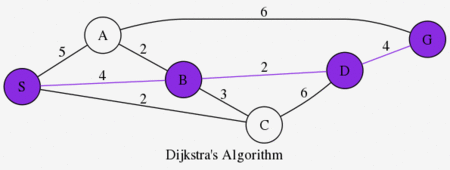
図におけるＳ点からＧ点に到達するための最短経路を求めたい。各ノードを結ぶエッジを糸としてＳ点をゆっくりと持ち上げた場合、緊張する糸が変移しながら最終的にＳ－Ｂ－Ｄ－Ｇを結ぶ糸が緊張して、これが最短経路と分かる¹。

計算機上でこの現象をシミュレートしたものを、ダイクストラ法というらしい。

今各ノードとそこから伸びるエッジの情報(コストと接続先)を渡して、その最短経路および総コストを出力するプログラムを考えてみよう。

data = {
 :s => [[5, :a], [4, :b], [2, :c]],
 :a => [[5, :s], [2, :b], [6, :g]],
 :b => [[4, :s], [2, :a], [3, :c], [2, :d]],
 :c => [[2, :s], [3, :b], [6, :d]],
 :d => [[2, :b], [6, :c], [4, :g]],
 :g => [[6, :a], [4, :d]]
 }
g = Graph.new(data)
g.print_route(:s, :g) # => s(0) -> b(4) -> d(6) -> g(10)

各ノードをエッジ情報を備えたNodeクラスのオブジェクトとし、エッジ情報をEdgeクラスのオブジェクトとしてそれぞれ表現し、Graphクラス内で生成するようにしよう。

各ノードオブジェクトには経路探索の経過および結果を保持するため、cost, done(確定ノードフラグ), from(直前ノードid)を用意する。

class Node
  attr_accessor :id, :edges, :cost, :done, :from
  def initialize(id, edges=[], cost=nil, done=false)
    @id, @edges, @cost, @done = id, edges, cost, done
  end
end
class Edge
  attr_reader :cost, :nid
  def initialize(cost, nid)
    @cost, @nid = cost, nid
  end
end
class Graph
  def initialize(data)
    @nodes =
      data.map do |id, edges|
        edges.map! { |edge| Edge.new(*edge) }
        Node.new(id, edges)
      end
  end
end

スタートsidからゴールgidまでの最短経路を求めるrouteメソッドと、その印刷用のprint_routeを定義しよう。

class Graph
  def route(sid, gid)
    dijkstra(sid)
    base = @nodes.find { |node| node.id == gid }
    @res = [base]
    while base = @nodes.find { |node| node.id == base.from }
      @res << base
    end
    @res
  end
  def print_route(sid, gid)
    route(sid, gid)
    puts @res.reverse.map { |node| "#{node.id}(#{node.cost})" }.join(" -> ")
  end
end

任意点nidのコストを求めるcostメソッドも定義しよう。

class Graph
  def cost(nid, sid)
    dijkstra(sid)
    @nodes.find { |node| node.id == nid }.cost		
  end
end

そして探索アルゴリズムの核心であるdijkstraメソッドを定義しよう。

class Graph
  private
  def dijkstra(sid)
    @nodes.each do |node|
      node.cost = node.id == sid ? 0 : nil
      node.done = false
      node.from = nil
    end
    loop do
      done_node = nil
      @nodes.each do |node|
        next if node.done or node.cost.nil?
        done_node = node if done_node.nil? or node.cost < done_node.cost
      end
      break unless done_node
      done_node.done = true
      done_node.edges.each do |edge|
        to = @nodes.find{ |node| node.id == edge.nid }
        cost = done_node.cost + edge.cost
        from = done_node.id
        if to.cost.nil? || cost < to.cost
          to.cost = cost 
          to.from = from
        end
      end
    end
  end
end

dijkstraメソッドでは次の処理をする。

スタートノードにコスト0をセットする
確定ノードdone_nodeに最少コストのノードをセットする
確定ノードのエッジの中からその接続先への総コストが最小となるよう接続先のコストを更新する
未確定ノードがなくなるまで(2)(3)を繰り返す

じゃあデータを入れてみよう！

data = {
 :s => [[5, :a], [4, :b], [2, :c]],
 :a => [[5, :s], [2, :b], [6, :g]],
 :b => [[4, :s], [2, :a], [3, :c], [2, :d]],
 :c => [[2, :s], [3, :b], [6, :d]],
 :d => [[2, :b], [6, :c], [4, :g]],
 :g => [[6, :a], [4, :d]]
 }
g = Graph.new(data)
g.print_route(:s, :g)
puts g.cost(:d, :s)
g.print_route(:a, :c)
# >> s(0) -> b(4) -> d(6) -> g(10)
# >> 6
# >> a(0) -> b(2) -> c(5)

いいみたいだ。

試験問題

Graphクラスがあればあの試験問題が解けるはずだ。まずは方針を考えよう。

迷路データを二次元配列として読み込む
迷路上の各マス(スペースの箇所)をその座標がidである²ノードオブジェクトとしてノードデータを生成しGraphオブジェクトを生成する
最短ルートを求め該当ノードを＄マークに置き換えた迷路を出力する

まずは迷路を読み込もう。

maze = DATA.readlines.map { |line| line.chomp.split(//) }
__END__
###************************
*S* *                    *
* * *  *  *************  *
* *   *    ************  *
*    *                   *
###************ ***********
*                        *
### ***********************
*      *              G  *
*  *      *********** *  *
*    *        ******* *  *
*       *                *
###************************

次にその座標がidになるようにノードデータを作り、それをGraphクラスに渡そう。

隣接するノードのデータedgesを作るのにちょっと工夫がいる。

nodes = {}
maze.each.with_index do |line, y|
  line.each.with_index do |data, x|
    next if data == '*'
    id = data.match(/\w/) ? $& : "#{y}_#{x}"
    edges =
      [[-1, 0], [1, 0], [0, -1], [0, 1]].inject([]) do |mem, (_y, _x)|
        _x += x; _y += y
        case maze[_y][_x]
        when /\w/ then mem << $&
        when /\s/ then mem << "#{_y}_#{_x}"
        else mem
        end
      end.map { |nid| [1, nid] }
    nodes[id] = edges
  end
end
g = Graph.new(nodes)

最後に最短経路を求めて、元の迷路データ上に＄マークをマッピングしよう。

route = g.route('S', 'G')
maze.each_with_index do |line, y|
  line.each_with_index do |data, x|
    print route.find { |pos| pos.id == "#{y}_#{x}" } ? '$' : data
  end
  print "\n"
end

###************************
*S* *$$$$$               *
*$* *$ * $*************  *
*$*$$$*  $$************  *
*$$$ *    $$$$$          *
###************$***********
* $$$$$$$$$$$$$          *
###$***********************
* $$$$$*$$$$$$$$$$$$$$G  *
*  *  $$$ *********** *  *
*    *        ******* *  *
*       *                *
###************************

なんかよさげだ。

http://gist.github.com/282664

参考：

ダイクストラ法（最短経路問題）ダイクストラ法 - Wikipedia

http://ja.wikipedia.org/wiki/%E3%83%80%E3%82%A4%E3%82%AF%E3%82%B9%E3%83%88%E3%83%A9%E6%B3%95 ↩
スタートとゴールはその文字 ↩

blog comments powered by Disqus

100円〜で好評発売中！
M'ELBORNE BOOKS