Rubyでビックリ階乗を解こう! 人間の実働時間を最適化する
「ビックリ階乗(Exclamatory Factorial)」って知ってますか?
ええ、知るわけないです。なぜならいま僕が、次のツイートの解に命名したばかりの言葉だからです1。
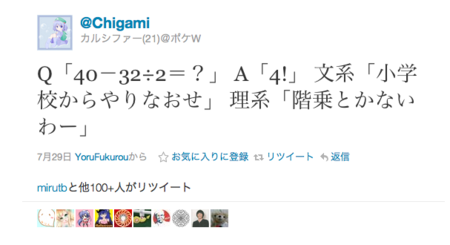
なかなか意味深なツイートですが、自分が先生だったらこの解答に◯を付けざるを得ないでしょう。答えにビックリマークを付ける人はいませんからね!
さて、プログラムする身としては文系理系両者の反応よりも、このような「ビックリ階乗」がどれくらい奇跡的なものなのかが気になります。つまりa - (b / c) の解(先の例では24)と、(a - b) / c の解の階乗(4!)とが一致する組み合わせは果たしてどれくらいあるのでしょうか。
数学的に書くとこういうことです。
そんな思いは当然僕だけではありませんでした2。
「40 - 32 / 2 = 4!」 - エンジニアのソフトウェア的愛情
このブログより1000以下の数字で、15組のビックリ階乗があることがわかっています。ここで1000までの数を考えたときa b c の組み合わせ数は、10億通り( 1000^3 )にもなりますからその確率は..
ビックリ階乗は奇跡的な組み合わせなんですね!
しかしそれにしても10億通りの組み合わせとなると、まじめにそのすべてを試してみると当然にその実行時間が問題になります。先のブログでは試行錯誤して最初のプログラムから、1800倍の高速化を実現して0.1秒以下で答えがでます。手元でRuby版も試して見ましたが0.037秒でした。ステキすぎます!
で、これ以上僕のできることは何も無いのですが、コードの実行時間というものを完全に無視してコードの読み易さつまり、人間の実働時間の最適化という一点に焦点を合わせてRubyでコードを書いてみようと思います^ ^;
さて、ビックリ階乗の数式をもう一度確認します。
これをRubyの式に置き換えます。
f1 = ->a,b,c{ a - b / c }
f2 = ->a,b,c{ (a - b) / c }
a, b, c = 40, 32, 2
f1[a,b,c] == factorial(f2[a,b,c]) # => trueメソッドでもいいですが、ここでは一行で済むProcを使います。
このコードは一見よさそうですが、一部に問題があります。
10 / 3 # => 3そうです、Rubyでは整数同士の除算は余りを無視してしまいます。
しかしこの問題はrequire 'mathn'することで解決します。
require 'mathn'
10 / 3 # => (10/3)次にfactorialメソッドってのがダサいですね。こうしましょう。
class Integer
def !
(1..self).inject(:*)
end
end
4.! # => 24require 'mathn'
f1 = ->a,b,c{ a - b / c }
f2 = ->a,b,c{ (a - b) / c }
a, b, c = 40, 32, 2
f1[a,b,c] == f2[a,b,c].! # => true良くなりましたね!
次にa b c についての10億の組み合わせを作ります。
set = [*2..1000].repeated_permutation(3) # => #<Enumerator: [2, 3, 4..]:repeated_permutation(3)>そこから先の条件に見合うものだけ、セレクトします。
selected = set.select { |abc| f1[*abc] == f2[*abc].! }結果をプリントします。
pp = ->abc{
print "(%i - %i) / %i = %i\n" % [*abc, f2[*abc]]
print " %i - %i / %i = %i! = %i\n\n" % [*abc, f2[*abc], f1[*abc]]
}
selected.each { |abc| pp[abc] }さあこれらを組み合わせて!
require "mathn"
class Integer
def !
(1..self).inject(:*)
end
end
f1 = ->a,b,c{ a - b / c }
f2 = ->a,b,c{ (a - b) / c }
pp = ->abc{
print "(%i - %i) / %i = %i\n" % [*abc, f2[*abc]]
print " %i - %i / %i = %i! = %i\n\n" % [*abc, f2[*abc], f1[*abc]]
}
[*2..1000].repeated_permutation(3)
.select { |abc| f1[*abc] == f2[*abc].! }
.each { |abc| pp[abc] }完成です! exclamation.rbで保存して実行してみましょう!いきなり1000もなんですから、まずは[*2..100]から..
% time ruby exclamation.rb
(25 - 5) / 5 = 4
25 - 5 / 5 = 4! = 24
(30 - 18) / 3 = 4
30 - 18 / 3 = 4! = 24
(40 - 32) / 2 = 4
40 - 32 / 2 = 4! = 24
ruby exclamation.rb 3.25s user 0.03s system 99% cpu 3.287 totalおおっ、良い感じじゃないですか!
では1000で..
% time ruby exclamation.rb
...
...
...全く反応ありません^ ^;
仕方が無いので、require ‘mathn’ はやめて、a <= b, (b % c) != 0, ((a - b) % c) != 0の条件だけ入れて足切りします。
[*2..1000].repeated_permutation(3)
.select { |a,b,c|
next if a <= b || (b % c) != 0 || ((a - b) % c) != 0
f1[a,b,c] == f2[a,b,c].!
}
.each { |abc| pp[abc] }いざ!
% time ruby exclamation.rb
...
...ちょっとトイレ行ってきます..
% time ruby exclamation.rb
...
...お茶飲んできます..
でましたよ!
(25 - 5) / 5 = 4
25 - 5 / 5 = 4! = 24
(30 - 18) / 3 = 4
30 - 18 / 3 = 4! = 24
(40 - 32) / 2 = 4
40 - 32 / 2 = 4! = 24
(138 - 108) / 6 = 5
138 - 108 / 6 = 5! = 120
(230 - 220) / 2 = 5
230 - 220 / 2 = 5! = 120
(721 - 103) / 103 = 6
721 - 103 / 103 = 6! = 720
(728 - 416) / 52 = 6
728 - 416 / 52 = 6! = 720
(731 - 473) / 43 = 6
731 - 473 / 43 = 6! = 720
(735 - 525) / 35 = 6
735 - 525 / 35 = 6! = 720
(748 - 616) / 22 = 6
748 - 616 / 22 = 6! = 720
(756 - 648) / 18 = 6
756 - 648 / 18 = 6! = 720
(765 - 675) / 15 = 6
765 - 675 / 15 = 6! = 720
(816 - 768) / 8 = 6
816 - 768 / 8 = 6! = 720
(833 - 791) / 7 = 6
833 - 791 / 7 = 6! = 720
(952 - 928) / 4 = 6
952 - 928 / 4 = 6! = 720
ruby exclamation.rb 349.56s user 0.72s system 99% cpu 5:51.87 total6分!!!
使い捨てプログラムとしては許容できる範囲… 判断は各人にお任せします..
blog comments powered by Disqus
