Rubyのinjectで東京までの最短経路を解くYO!

「すごいHaskellたのしく学ぼう!」の第10章に、Haskellを使って「ヒースロー空港からロンドンへの最適経路(optimal path)」を算出する例が出ていました。例ではその実現に畳み込み演算が使われていたので、前回同様、Rubyでもinjectを使ってこの問題を解いてみたいと思います。アヒル脳じゃなかなかHaskellの世界に入っていけませんよー。

オリジナルの解説（英語）とHaskellによる解法は、以下にあります。

Functionally Solving Problems - Learn You a Haskell for Great Good!

問題

問題設定は次のようなものです。

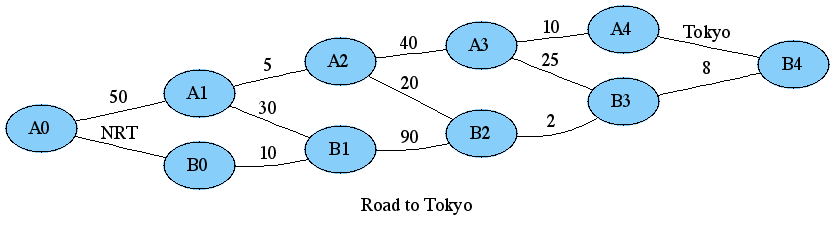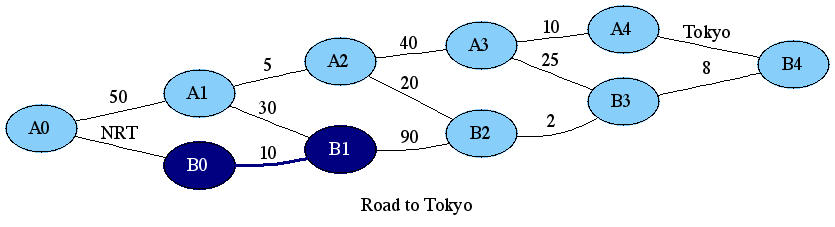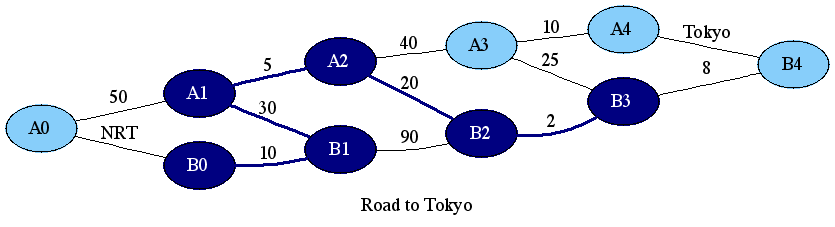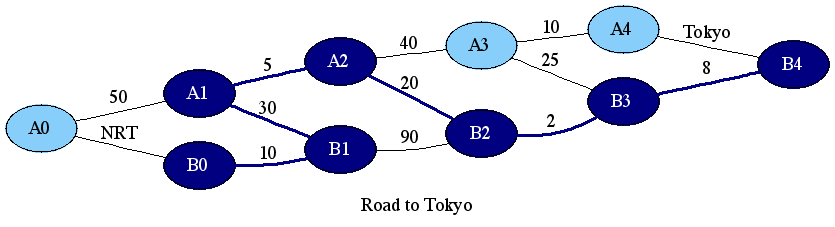
1. 成田空港（NRT）から東京（Tokyo）に向かう２本の幹線道路A,Bがある。
2. 途中にこれらを橋渡しする３本の地方道路Cがある。
3. 地方道路で区切られる各道路セグメントの通過に掛かる所要時間は決まっている（図を参照）。
4. 成田（A0またはB0）から出発して最短で東京（A4またはB4）に到達できる経路を求めよ。

Alt road to tokyo noshadow

方針

基本的な考え方は「すごいHaskellたのしく学ぼう!」から頂戴しまして（^ ^;）、これをオブジェクト指向的に解いていきます。

解法は再帰的手法を使います。つまり直近の交差点に到達する最適経路を求め、同じ処理を順次先の交差点に適用して最終地点に至るという方法です。具体的には次のようになります。

1. A0またはB0から出発して`A1`に至る最短経路を決める。 => B0 -> B1 -> A1 (10 + 30 = 40 min)
2. A0またはB0から出発して`B1`に至る最短経路を決める。 => B0 -> B1 (10 min)
3. A1またはB1から出発して`A2`に至る最短経路を決める。 => A1 -> A2 (5 min)
4. A1またはB1から出発して`B2`に至る最短経路を決める。 => A1 -> A2 -> B2 ( 5 + 20 = 25 min)

上記３において、その基点であるA1に至る最短経路は、１においてB0 -> B1 -> A1(40 min)と決まっているので、出発点からA2に至る最短経路は、B0 -> B1 -> A1 -> A2(40 + 5 = 45 min)と決まることになります。また、上記４においても同様に、A1までの最短経路が決まっているので、出発点からB2に至る最短経路は、B0 -> B1 -> A1 -> A2 -> B2 (40 + 25 = 65 min)と決まることになります。これを繰り返せば目的地であるA4およびB4への最短経路がわかることになります。そして、最後にA4とB4の何れか短い経路を選択することによって、回答が得られます。

出力イメージ

最初に、最終的な出力をイメージします。OptimalPathクラスを用意して設定条件を渡し、solveメソッドを実行すると最短経路が出力される、そんなイメージでいきます。

op = OptimalPath.new(nrt_to_tokyo)
op.solve # => [(B, 10), (C, 30), (A, 5), (C, 20), (B, 2), (B, 8)]

出力の[(B, 10), (C, 30)...]というのは、「Bを10分走って、Cを30分走って..」という感じです。

渡される設定条件は、injectで処理しやすいように道路セグメントをグループ化して渡します。このグループをsectionとします。

Section = Struct.new(:a, :b, :c)

nrt_to_tokyo = 
  [ [50,10,30],
    [ 5,90,20],
    [40, 2,25],
    [10, 8, 0]
   ].map { |a,b,c| Section[a,b,c] }

nrt_to_tokyo # => [#<struct Section a=50, b=10, c=30>, #<struct Section a=5, b=90, c=20>, #<struct Section a=40, b=2, c=25>, #<struct Section a=10, b=8, c=0>]

op = OptimalPath.new(nrt_to_tokyo)
op.solve # => [(B, 10), (C, 30), (A, 5), (C, 20), (B, 2), (B, 8), (C, 0)]

OptimalPath

OptimalPathクラスを実装します。設定条件road_systemを受け取って、solveメソッドで最適経路を出力するのでしたね。

class OptimalPath
  def initialize(road_system)
    @road_system = road_system
  end

  def solve
    bestA, bestB =
      @road_system.inject([Path.new, Path.new]) do |(pathA, pathB), section|
        road_step(pathA, pathB, section)
      end
    [bestA, bestB].min_by(&:length)
  end

  def road_step(pathA, pathB, section)
  end
end

solveにおいては、Enumerable#injectを使って各セッションを順次処理していきます。ここで、A4とB4までの最短経路を管理するために2つのPathオブジェクトを用意します。injectにおけるイテレーションが繰り返されて最終的に、A4とB4に至る最短経路が出力されるので、そのより短いものを選択します。

Segmentクラス

road_stepの実装は後にして、次にSegmentクラスを実装します。Segmentクラスは個々の道路セグメントを表すクラスです。各SegmentオブジェクトはA~Cのラベル（label）と通過時間（length）を持ちます。

class OptimalPath
  class Segment
    def self.[](label, length)
      new(label, length)
    end

    attr_reader :label, :length
    def initialize(label, length)
      @label, @length = label, length
    end

    def to_s
      "(#{label}, #{length})"
    end
  end

  seg_a10 = Segment[:A, 10] # => (A, 10)
  seg_c30 = Segment[:C, 30] # => (C, 30)
  seg_a10.length # => 10
  seg_c30.length # => 30
end

Segment.[]クラスメソッドを定義して、オブジェクトの生成をArrayライクにできるようにします。

Pathクラス

次に、最適経路を管理するためのPathクラスを実装します。Pathクラスは、複数のSegmentオブジェクト管理する配列のようなクラスです。

class OptimalPath
  class Path
    def initialize(segment=nil)
      @path = segment ? segment : []
    end

    def +(segment)
      self.class.new(@path + segment)
    end

    def length
      @path.map(&:length).inject(0, :+)
    end

    def to_s
      "#{@path}"
    end
  end

  path = Path.new
  path.length # => 0
  path1 = path + [Segment[:B, 10], Segment[:C, 30]]
  path1.length # => 40
end

Path#+は新たなSegmentを追加した新たなPathオブジェクトを生成します。Path#lengthはPath内のSegmentの通過時間の合計を返します。

road_stepの実装

さて下準備ができたので、OptimalPathクラスに戻って、実装のコアであるroad_stepメソッドを実装します。先に示したようにroad_stepは、solveメソッドのinject内において、各セクションを受け取ってそのセクションまでの２つの最適経路を計算して返します。実装は次にようになります。

class OptimalPath
  def initialize(road_system)
    @road_system = road_system
  end

  def solve
    bestA, bestB =
      @road_system.inject([Path.new, Path.new]) do |(pathA, pathB), section|
        road_step(pathA, pathB, section)
      end
    [bestA, bestB].min_by(&:length)
  end

  def road_step(pathA, pathB, section)
    a, b, c = section.values
    candidatesA = [ pathA + [ Segment[:A, a] ], 
                    pathB + [ Segment[:B, b], Segment[:C, c] ]]
    candidatesB = [ pathB + [ Segment[:B, b] ],
                    pathA + [ Segment[:A, a], Segment[:C, c] ]]
    
    pathA = candidatesA.min_by { |path| path.length }
    pathB = candidatesB.min_by { |path| path.length }
    [pathA, pathB]
  end
end

道路A側の交差点(例えばA2)における最適経路は、直前のA側の点(A1)までの最適経路pathAにそこからの道路セグメント[(:A, 5)]を足したものか、直前のB側の点(B1)までの最適経路pathBにそこからの道路セグメント[(:B, 90)(:C, 20)]を足したもの、のいずれかです(candidatesA)。そして、そこからその総経過時間の短い方をmin_byで取得すれば、道路A側の最適経路が求まります。道路B側も同様です。

さあこれで実装が終わりました。全コードを再掲します。

いいですね！

やっぱりinject、最強ですよね？

YOUたち!RubyでinjectしちゃいなYO!

Rubyのinjectで逆ポーランド記法電卓を書くYO!

すごいHaskellたのしく学ぼう! by Miran Lipovača